The Class 7 is an important year in a student’s life and Maths is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 7 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete NCERT Class 7 Maths Book syllabus.
Exercise 12.1 Page: 234
1. Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.
(i) Subtraction of z from y.
Solution:-
= Y – z
(ii) One-half of the sum of numbers x and y.
Solution:-
= ½ (x + y)
= (x + y)/2
(iii) The number z multiplied by itself.
Solution:-
= z × z
= z2
(iv) One-fourth of the product of numbers p and q.
Solution:-
= ¼ (p × q)
= pq/4
(v) Numbers x and y, both squared and added.
Solution:-
= x2 + y2
(vi) Number 5 added to three times the product of numbers m and n.
Solution:-
= 3mn + 5
(vii) Product of numbers y and z subtracted from 10.
Solution:-
= 10 – (y × z)
= 10 – yz
(viii) Sum of numbers a and b subtracted from their product.
Solution:-
= (a × b) – (a + b)
= ab – (a + b)
2. (i) Identify the terms and their factors in the following expressions.
Show the terms and factors by tree diagrams.
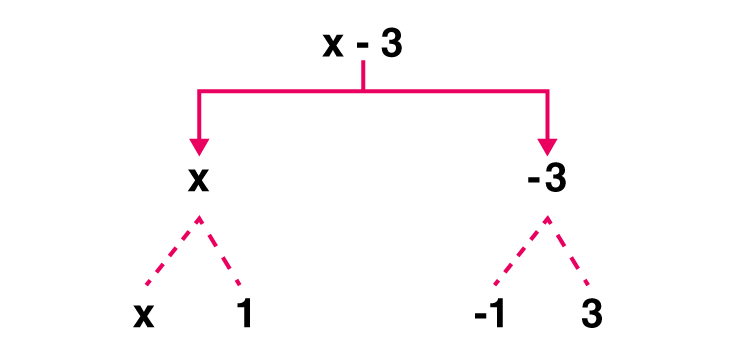
(a) x – 3
Solution:-
Expression: x – 3
Terms: x, -3
Factors: x; -3
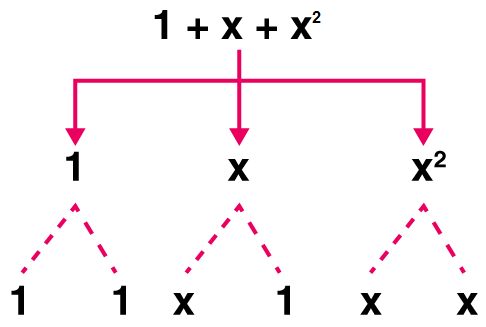
(b) 1 + x + x2
Solution:-
Expression: 1 + x + x2
Terms: 1, x, x2
Factors: 1; x; x,x
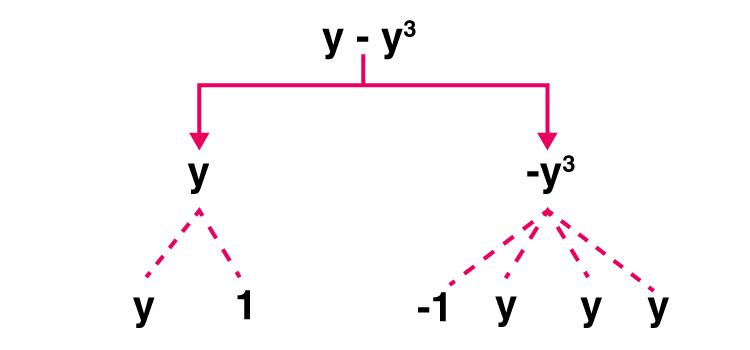
(c) y – y3
Solution:-
Expression: y – y3
Terms: y, -y3
Factors: y; -y, -y, -y
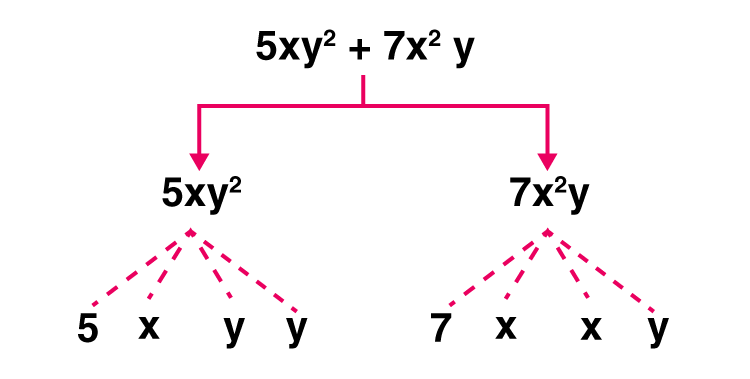
(d) 5xy2 + 7x2 y
Solution:-
Expression: 5xy2 + 7x2 y
Terms: 5xy2 , 7x2 y
Factors: 5, x, y, y; 7, x, x, y
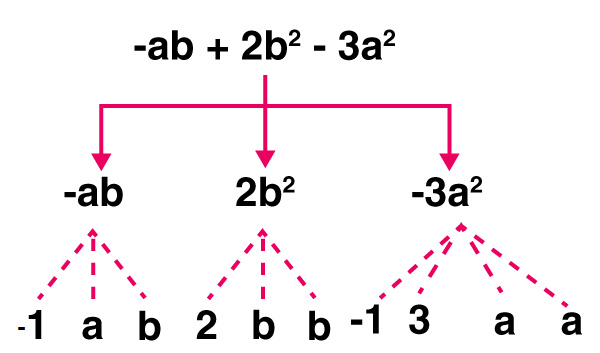
(e) – ab + 2b2 – 3a2
Solution:-
Expression: -ab + 2b2 – 3a2
Terms: -ab, 2b2 , -3a2
Factors: -a, b; 2, b, b; -3, a, a
(ii) Identify terms and factors in the expressions given below.
(a) – 4x + 5 (b) – 4x + 5y (c) 5y + 3y2 (d) xy + 2x2 y2
(e) pq + q (f) 1.2 ab – 2.4 b + 3.6 a (g) ¾ x + ¼
(h) 0.1 p2 + 0.2 q2
Solution:-
Expressions are defined as numbers, symbols and operators (such as +. – , × and ÷) grouped together that show the value of something.
In algebra, a term is either a single number or variable or numbers and variables multiplied together. Terms are separated by + or – signs or sometimes by division.
Factors are defined as numbers we can multiply together to get another number.
| Sl.No. | Expression | Terms | Factors |
| (a) | – 4x + 5 |
-4x
5 |
-4, x
5 |
| (b) | – 4x + 5y |
-4x
5y |
-4, x
5, y |
| (c) | 5y + 3y2 |
5y
3y2 |
5, y
3, y, y |
| (d) | xy + 2x2 y2 |
xy
2x2 y2 |
x, y
2, x, x, y, y |
| (e) | pq + q |
pq
q |
P, q
Q |
| (f) | 1.2 ab – 2.4 b + 3.6 a |
1.2ab
-2.4b 3.6a |
1.2, a, b
-2.4, b 3.6, a |
| (g) | ¾ x + ¼ |
¾ x
¼ |
¾, x
¼ |
| (h) | 0.1 p2 + 0.2 q2 |
0.1p2
0.2q2 |
0.1, p, p
0.2, q, q |
3. Identify the numerical coefficients of terms (other than constants) in the following expressions.
(i) 5 – 3t2 (ii) 1 + t + t2 + t3 (iii) x + 2xy + 3y (iv) 100m + 1000n (v) – p2 q2 + 7pq (vi) 1.2 a + 0.8 b (vii) 3.14 r2 (viii) 2 (l + b)
(ix) 0.1 y + 0.01 y2
Solution:-
Expressions are defined as numbers, symbols and operators (such as +. – , × and ÷) grouped together that show the value of something.
In algebra, a term is either a single number or variable or numbers and variables multiplied together. Terms are separated by + or – signs or sometimes by division.
A coefficient is a number used to multiply a variable (2x means 2 times x, so 2 is a coefficient). Variables on their own (without a number next to them) actually have a coefficient of 1 (x is really 1x).
| Sl.No. | Expression | Terms | Coefficients |
| (i) | 5 – 3t2 | – 3t2 | -3 |
| (ii) | 1 + t + t2 + t3 |
t
t2 t3 |
1
1 1 |
| (iii) | x + 2xy + 3y |
x
2xy 3y |
1
2 3 |
| (iv) | 100m + 1000n |
100m
1000n |
100
1000 |
| (v) | – p2 q2 + 7pq |
-p2
q2
7pq |
-1
7 |
| (vi) | 1.2 a + 0.8 b |
1.2a
0.8b |
1.2
0.8 |
| (vii) | 3.14 r2 | 3.142 | 3.14 |
| (viii) | 2 (l + b) |
2l
2b |
2
2 |
| (ix) | 0.1 y + 0.01 y2 |
0.1y
0.01y2 |
0.1
0.01 |
4. (a) Identify terms which contain x and give the coefficient of x.
(i) y2 x + y (ii) 13y2 – 8yx (iii) x + y + 2
(iv) 5 + z + zx (v) 1 + x + xy (vi) 12xy2 + 25
(vii) 7x + xy2
Solution:-
| Sl.No. | Expression | Terms | Coefficient of x |
| (i) | y2 x + y | y2 x | y2 |
| (ii) | 13y2 – 8yx | – 8yx | -8y |
| (iii) | x + y + 2 | x | 1 |
| (iv) | 5 + z + zx |
x
zx |
1
z |
| (v) | 1 + x + xy | xy | y |
| (vi) | 12xy2 + 25 | 12xy2 | 12y2 |
| (vii) | 7x + xy2 |
7x
xy2 |
7
y2 |
(b) Identify terms which contain y2 and give the coefficient of y2 .
(i) 8 – xy2 (ii) 5y2 + 7x (iii) 2x2 y – 15xy2 + 7y2
Solution:-
| Sl.No. | Expression | Terms | Coefficient of y2 |
| (i) | 8 – xy2 | – xy2 | – x |
| (ii) | 5y2 + 7x | 5y2 | 5 |
| (iii) | 2x2 y – 15xy2 + 7y2 |
– 15xy2
7y2 |
– 15x
7 |
5. Classify into monomials, binomials and trinomials.
(i) 4y – 7z
Solution:-
Binomial.
An expression which contains two unlike terms is called a binomial.
(ii) y2
Solution:-
Monomial.
An expression with only one term is called a monomial.
(iii) x + y – xy
Solution:-
Trinomial.
An expression which contains three terms is called a trinomial.
(iv) 100
Solution:-
Monomial.
An expression with only one term is called a monomial.
(v) ab – a – b
Solution:-
Trinomial.
An expression which contains three terms is called a trinomial.
(vi) 5 – 3t
Solution:-
Binomial.
An expression which contains two unlike terms is called a binomial.
(vii) 4p2 q – 4pq2
Solution:-
Binomial.
An expression which contains two unlike terms is called a binomial.
(viii) 7mn
Solution:-
Monomial.
An expression with only one term is called a monomial.
(ix) z2 – 3z + 8
Solution:-
Trinomial.
An expression which contains three terms is called a trinomial.
(x) a2 + b2
Solution:-
Binomial.
An expression which contains two unlike terms is called a binomial.
(xi) z2 + z
Solution:-
Binomial.
An expression which contains two unlike terms is called a binomial.
(xii) 1 + x + x2
Solution:-
Trinomial.
An expression which contains three terms is called a trinomial.
6. State whether a given pair of terms is of like or unlike terms.
(i) 1, 100
Solution:-
Like term.
When terms have the same algebraic factors, they are like terms.
(ii) –7x, (5/2)x
Solution:-
Like term.
When terms have the same algebraic factors, they are like terms.
(iii) – 29x, – 29y
Solution:-
Unlike terms.
The terms have different algebraic factors, they are unlike terms.
(iv) 14xy, 42yx
Solution:-
Like term.
When terms have the same algebraic factors, they are like terms.
(v) 4m2 p, 4mp2
Solution:-
Unlike terms.
The terms have different algebraic factors, they are unlike terms.
(vi) 12xz, 12x2 z2
Solution:-
Unlike terms.
The terms have different algebraic factors, they are unlike terms.
7. Identify like terms in the following.
(a) – xy2 , – 4yx2 , 8x2 , 2xy2 , 7y, – 11x2 , – 100x, – 11yx, 20x2 y, – 6x2 , y, 2xy, 3x
Solution:-
When terms have the same algebraic factors, they are like terms.
They are,
– xy2 , 2xy2
– 4yx2 , 20x2 y
8x2 , – 11x2 , – 6x2
7y, y
– 100x, 3x
– 11yx, 2xy
(b) 10pq, 7p, 8q, – p2 q2 , – 7qp, – 100q, – 23, 12q2 p2 , – 5p2 , 41, 2405p, 78qp,
13p2 q, qp2 , 701p2
Solution:-
When terms have the same algebraic factors, they are like terms.
They are,
10pq, – 7qp, 78qp
7p, 2405p
8q, – 100q
– p2 q2 , 12q2 p2
– 23, 41
– 5p2 , 701p2
13p2 q, qp2
Exercise 12.2 Page: 239
1. Simplify combining like terms.
(i) 21b – 32 + 7b – 20b
Solution:-
When terms have the same algebraic factors, they are like terms.
Then,
= (21b + 7b – 20b) – 32
= b (21 + 7 – 20) – 32
= b (28 – 20) – 32
= b (8) – 32
= 8b – 32
(ii) – z2 + 13z2 – 5z + 7z3 – 15z
Solution:-
When terms have the same algebraic factors, they are like terms.
Then,
= 7z3 + (-z2 + 13z2 ) + (-5z – 15z)
= 7z3 + z2 (-1 + 13) + z (-5 – 15)
= 7z3 + z2 (12) + z (-20)
= 7z3 + 12z2 – 20z
(iii) p – (p – q) – q – (q – p)
Solution:-
When terms have the same algebraic factors, they are like terms.
Then,
= p – p + q – q – q + p
= p – q
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
Solution:-
When terms have the same algebraic factors, they are like terms.
Then,
= 3a – 2b – ab – a + b – ab + 3ab + b – a
= 3a – a – a – 2b + b + b – ab – ab + 3ab
= a (1 – 1- 1) + b (-2 + 1 + 1) + ab (-1 -1 + 3)
= a (1 – 2) + b (-2 + 2) + ab (-2 + 3)
= a (1) + b (0) + ab (1)
= a + ab
(v) 5x2 y – 5x2 + 3yx2 – 3y2 + x2 – y2 + 8xy2 – 3y2
Solution:-
When terms have the same algebraic factors, they are like terms.
Then,
= 5x2 y + 3yx2 – 5x2 + x2 – 3y2 – y2 – 3y2
= x2 y (5 + 3) + x2 (- 5 + 1) + y2 (-3 – 1 -3) + 8xy2
= x2 y (8) + x2 (-4) + y2 (-7) + 8xy2
= 8x2 y – 4x2 – 7y2 + 8xy2
(vi) (3y2 + 5y – 4) – (8y – y2 – 4)
Solution:-
When terms have the same algebraic factors, they are like terms.
Then,
= 3y2 + 5y – 4 – 8y + y2 + 4
= 3y2 + y2 + 5y – 8y – 4 + 4
= y2 (3 + 1) + y (5 – 8) + (-4 + 4)
= y2 (4) + y (-3) + (0)
= 4y2 – 3y
2. Add:
(i) 3mn, – 5mn, 8mn, – 4mn
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to add the like terms.
= 3mn + (-5mn) + 8mn + (- 4mn)
= 3mn – 5mn + 8mn – 4mn
= mn (3 – 5 + 8 – 4)
= mn (11 – 9)
= mn (2)
= 2mn
(ii) t – 8tz, 3tz – z, z – t
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to add the like terms.
= t – 8tz + (3tz – z) + (z – t)
= t – 8tz + 3tz – z + z – t
= t – t – 8tz + 3tz – z + z
= t (1 – 1) + tz (- 8 + 3) + z (-1 + 1)
= t (0) + tz (- 5) + z (0)
= – 5tz
(iii) – 7mn + 5, 12mn + 2, 9mn – 8, – 2mn – 3
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to add the like terms.
= – 7mn + 5 + 12mn + 2 + (9mn – 8) + (- 2mn – 3)
= – 7mn + 5 + 12mn + 2 + 9mn – 8 – 2mn – 3
= – 7mn + 12mn + 9mn – 2mn + 5 + 2 – 8 – 3
= mn (-7 + 12 + 9 – 2) + (5 + 2 – 8 – 3)
= mn (- 9 + 21) + (7 – 11)
= mn (12) – 4
= 12mn – 4
(iv) a + b – 3, b – a + 3, a – b + 3
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to add the like terms.
= a + b – 3 + (b – a + 3) + (a – b + 3)
= a + b – 3 + b – a + 3 + a – b + 3
= a – a + a + b + b – b – 3 + 3 + 3
= a (1 – 1 + 1) + b (1 + 1 – 1) + (-3 + 3 + 3)
= a (2 -1) + b (2 -1) + (-3 + 6)
= a (1) + b (1) + (3)
= a + b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to add the like terms.
= 14x + 10y – 12xy – 13 + (18 – 7x – 10y + 8xy) + 4xy
= 14x + 10y – 12xy – 13 + 18 – 7x – 10y + 8xy + 4xy
= 14x – 7x + 10y– 10y – 12xy + 8xy + 4xy – 13 + 18
= x (14 – 7) + y (10 – 10) + xy(-12 + 8 + 4) + (-13 + 18)
= x (7) + y (0) + xy(0) + (5)
= 7x + 5
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to add the like terms.
= 5m – 7n + (3n – 4m + 2) + (2m – 3mn – 5)
= 5m – 7n + 3n – 4m + 2 + 2m – 3mn – 5
= 5m – 4m + 2m – 7n + 3n – 3mn + 2 – 5
= m (5 – 4 + 2) + n (-7 + 3) – 3mn + (2 – 5)
= m (3) + n (-4) – 3mn + (-3)
= 3m – 4n – 3mn – 3
(vii) 4x2 y, – 3xy2 , –5xy2 , 5x2 y
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to add the like terms.
= 4x2 y + (-3xy2 ) + (-5xy2 ) + 5x2 y
= 4x2 y + 5x2 y – 3xy2 – 5xy2
= x2 y (4 + 5) + xy2 (-3 – 5)
= x2 y (9) + xy2 (- 8)
= 9x2 y – 8xy2
(viii) 3p2 q2 – 4pq + 5, – 10 p2 q2 , 15 + 9pq + 7p2 q2
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to add the like terms.
= 3p2 q2 – 4pq + 5 + (- 10p2 q2 ) + 15 + 9pq + 7p2 q2
= 3p2 q2 – 10p2 q2 + 7p2 q2 – 4pq + 9pq + 5 + 15
= p2 q2 (3 -10 + 7) + pq (-4 + 9) + (5 + 15)
= p2 q2 (0) + pq (5) + 20
= 5pq + 20
(ix) ab – 4a, 4b – ab, 4a – 4b
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to add the like terms.
= ab – 4a + (4b – ab) + (4a – 4b)
= ab – 4a + 4b – ab + 4a – 4b
= ab – ab – 4a + 4a + 4b – 4b
= ab (1 -1) + a (4 – 4) + b (4 – 4)
= ab (0) + a (0) + b (0)
= 0
(x) x2 – y2 – 1, y2 – 1 – x2 , 1 – x2 – y2
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to add the like terms.
= x2 – y2 – 1 + (y2 – 1 – x2 ) + (1 – x2 – y2 )
= x2 – y2 – 1 + y2 – 1 – x2 + 1 – x2 – y2
= x2 – x2 – x2 – y2 + y2 – y2 – 1 – 1 + 1
= x2 (1 – 1- 1) + y2 (-1 + 1 – 1) + (-1 -1 + 1)
= x2 (1 – 2) + y2 (-2 +1) + (-2 + 1)
= x2 (-1) + y2 (-1) + (-1)
= -x2 – y2 -1
3. Subtract:
(i) –5y2 from y2
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms.
= y2 – (-5y2 )
= y2 + 5y2
= 6y2
(ii) 6xy from –12xy
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms.
= -12xy – 6xy
= – 18xy
(iii) (a – b) from (a + b)
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms.
= (a + b) – (a – b)
= a + b – a + b
= a – a + b + b
= a (1 – 1) + b (1 + 1)
= a (0) + b (2)
= 2b
(iv) a (b – 5) from b (5 – a)
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms.
= b (5 -a) – a (b – 5)
= 5b – ab – ab + 5a
= 5b + ab (-1 -1) + 5a
= 5a + 5b – 2ab
(v) –m2 + 5mn from 4m2 – 3mn + 8
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms.
= 4m2 – 3mn + 8 – (- m2 + 5mn)
= 4m2 – 3mn + 8 + m2 – 5mn
= 4m2 + m2 – 3mn – 5mn + 8
= 5m2 – 8mn + 8
(vi) – x2 + 10x – 5 from 5x – 10
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms.
= 5x – 10 – (-x2 + 10x – 5)
= 5x – 10 + x2 – 10x + 5
= x2 + 5x – 10x – 10 + 5
= x2 – 5x – 5
(vii) 5a2 – 7ab + 5b2 from 3ab – 2a2 – 2b2
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms.
= 3ab – 2a2 – 2b2 – (5a2 – 7ab + 5b2 )
= 3ab – 2a2 – 2b2 – 5a2 + 7ab – 5b2
= 3ab + 7ab – 2a2 – 5a2 – 2b2 – 5b2
= 10ab – 7a2 – 7b2
(viii) 4pq – 5q2 – 3p2 from 5p2 + 3q2 – pq
Solution:-
When terms have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms.
= 5p2 + 3q2 – pq – (4pq – 5q2 – 3p2 )
= 5p2 + 3q2 – pq – 4pq + 5q2 + 3p2
= 5p2 + 3p2 + 3q2 + 5q2 – pq – 4pq
= 8p2 + 8q2 – 5pq
4. (a) What should be added to x2 + xy + y2 to obtain 2x2 + 3xy?
Solution:-
Let us assume p be the required term.
Then,
p + (x2 + xy + y2 ) = 2x2 + 3xy
p = (2x2 + 3xy) – (x2 + xy + y2 )
p = 2x2 + 3xy – x2 – xy – y2
p = 2x2 – x2 + 3xy – xy – y2
p = x2 + 2xy – y2
(b) What should be subtracted from 2a + 8b + 10 to get – 3a + 7b + 16?
Solution:-
Let us assume x be the required term.
Then,
2a + 8b + 10 – x = -3a + 7b + 16
x = (2a + 8b + 10) – (-3a + 7b + 16)
x = 2a + 8b + 10 + 3a – 7b – 16
x = 2a + 3a + 8b – 7b + 10 – 16
x = 5a + b – 6
5. What should be taken away from 3x2 – 4y2 + 5xy + 20 to obtain – x2 – y2 + 6xy + 20?
Solution:-
Let us assume a be the required term.
Then,
3x2 – 4y2 + 5xy + 20 – a = -x2 – y2 + 6xy + 20
a = 3x2 – 4y2 + 5xy + 20 – (-x2 – y2 + 6xy + 20)
a = 3x2 – 4y2 + 5xy + 20 + x2 + y2 – 6xy – 20
a = 3x2 + x2 – 4y2 + y2 + 5xy – 6xy + 20 – 20
a = 4x2 – 3y2 – xy
6. (a) From the sum of 3x – y + 11 and – y – 11, subtract 3x – y – 11.
Solution:-
First, we have to find out the sum of 3x – y + 11 and – y – 11.
= 3x – y + 11 + (-y – 11)
= 3x – y + 11 – y – 11
= 3x – y – y + 11 – 11
= 3x – 2y
Now, subtract 3x – y – 11 from 3x – 2y.
= 3x – 2y – (3x – y – 11)
= 3x – 2y – 3x + y + 11
= 3x – 3x – 2y + y + 11
= -y + 11
(b) From the sum of 4 + 3x and 5 – 4x + 2x2 , subtract the sum of 3x2 – 5x and
–x2 + 2x + 5.
Solution:-
First, we have to find out the sum of 4 + 3x and 5 – 4x + 2x2
= 4 + 3x + (5 – 4x + 2x2 )
= 4 + 3x + 5 – 4x + 2x2
= 4 + 5 + 3x – 4x + 2x2
= 9 – x + 2x2
= 2x2 – x + 9 … [equation 1]
Then, we have to find out the sum of 3x2 – 5x and – x2 + 2x + 5
= 3x2 – 5x + (-x2 + 2x + 5)
= 3x2 – 5x – x2 + 2x + 5
= 3x2 – x2 – 5x + 2x + 5
= 2x2 – 3x + 5 … [equation 2]
Now, we have to subtract equation (2) from equation (1)
= 2x2 – x + 9 – (2x2 – 3x + 5)
= 2x2 – x + 9 – 2x2 + 3x – 5
= 2x2 – 2x2 – x + 3x + 9 – 5
= 2x + 4
Exercise 12.3 Page: 242
1. If m = 2, find the value of:
(i) m – 2
Solution:-
From the question, it is given that m = 2
Then, substitute the value of m in the question.
= 2 -2
= 0
(ii) 3m – 5
Solution:-
From the question, it is given that m = 2
Then, substitute the value of m in the question.
= (3 × 2) – 5
= 6 – 5
= 1
(iii) 9 – 5m
Solution:-
From the question, it is given that m = 2
Then, substitute the value of m in the question.
= 9 – (5 × 2)
= 9 – 10
= – 1
(iv) 3m2 – 2m – 7
Solution:-
From the question, it is given that m = 2
Then, substitute the value of m in the question.
= (3 × 22 ) – (2 × 2) – 7
= (3 × 4) – (4) – 7
= 12 – 4 -7
= 12 – 11
= 1
(v) (5m/2) – 4
Solution:-
From the question, it is given that m = 2
Then, substitute the value of m in the question.
= ((5 × 2)/2) – 4
= (10/2) – 4
= 5 – 4
= 1
2. If p = – 2, find the value of:
(i) 4p + 7
Solution:-
From the question, it is given that p = -2
Then, substitute the value of p in the question.
= (4 × (-2)) + 7
= -8 + 7
= -1
(ii) – 3p2 + 4p + 7
Solution:-
From the question, it is given that p = -2
Then, substitute the value of p in the question.
= (-3 × (-2)2 ) + (4 × (-2)) + 7
= (-3 × 4) + (-8) + 7
= -12 – 8 + 7
= -20 + 7
= -13
(iii) – 2p3 – 3p2 + 4p + 7
Solution:-
From the question, it is given that p = -2
Then, substitute the value of p in the question.
= (-2 × (-2)3 ) – (3 × (-2)2 ) + (4 × (-2)) + 7
= (-2 × -8) – (3 × 4) + (-8) + 7
= 16 – 12 – 8 + 7
= 23 – 20
= 3
3. Find the value of the following expressions when x = –1:
(i) 2x – 7
Solution:-
From the question, it is given that x = -1
Then, substitute the value of x in the question.
= (2 × -1) – 7
= – 2 – 7
= – 9
(ii) – x + 2
Solution:-
From the question, it is given that x = -1
Then, substitute the value of x in the question.
= – (-1) + 2
= 1 + 2
= 3
(iii) x2 + 2x + 1
Solution:-
From the question, it is given that x = -1
Then, substitute the value of x in the question.
= (-1)2 + (2 × -1) + 1
= 1 – 2 + 1
= 2 – 2
= 0
(iv) 2x2 – x – 2
Solution:-
From the question, it is given that x = -1
Then, substitute the value of x in the question.
= (2 × (-1)2 ) – (-1) – 2
= (2 × 1) + 1 – 2
= 2 + 1 – 2
= 3 – 2
= 1
4. If a = 2, b = – 2, find the value of:
(i) a2 + b2
Solution:-
From the question, it is given that a = 2, b = -2
Then, substitute the value of a and b in the question.
= (2)2 + (-2)2
= 4 + 4
= 8
(ii) a2 + ab + b2
Solution:-
From the question, it is given that a = 2, b = -2
Then, substitute the value of a and b in the question.
= 22 + (2 × -2) + (-2)2
= 4 + (-4) + (4)
= 4 – 4 + 4
= 4
(iii) a2 – b2
Solution:-
From the question, it is given that a = 2, b = -2
Then, substitute the value of a and b in the question.
= 22 – (-2)2
= 4 – (4)
= 4 – 4
= 0
5. When a = 0, b = – 1, find the value of the given expressions:
(i) 2a + 2b
Solution:-
From the question, it is given that a = 0, b = -1
Then, substitute the value of a and b in the question.
= (2 × 0) + (2 × -1)
= 0 – 2
= -2
(ii) 2a2 + b2 + 1
Solution:-
From the question, it is given that a = 0, b = -1
Then, substitute the value of a and b in the question.
= (2 × 02 ) + (-1)2 + 1
= 0 + 1 + 1
= 2
(iii) 2a2 b + 2ab2 + ab
Solution:-
From the question, it is given that a = 0, b = -1
Then, substitute the value of a and b in the question.
= (2 × 02 × -1) + (2 × 0 × (-1)2 ) + (0 × -1)
= 0 + 0 +0
= 0
(iv) a2 + ab + 2
Solution:-
From the question, it is given that a = 0, b = -1
Then, substitute the value of a and b in the question.
= (02 ) + (0 × (-1)) + 2
= 0 + 0 + 2
= 2
6. Simplify the expressions and find the value if x is equal to 2
(i) x + 7 + 4 (x – 5)
Solution:-
From the question, it is given that x = 2
We have,
= x + 7 + 4x – 20
= 5x + 7 – 20
Then, substitute the value of x in the equation.
= (5 × 2) + 7 – 20
= 10 + 7 – 20
= 17 – 20
= – 3
(ii) 3 (x + 2) + 5x – 7
Solution:-
From the question, it is given that x = 2
We have,
= 3x + 6 + 5x – 7
= 8x – 1
Then, substitute the value of x in the equation.
= (8 × 2) – 1
= 16 – 1
= 15
(iii) 6x + 5 (x – 2)
Solution:-
From the question, it is given that x = 2
We have,
= 6x + 5x – 10
= 11x – 10
Then, substitute the value of x in the equation.
= (11 × 2) – 10
= 22 – 10
= 12
(iv) 4(2x – 1) + 3x + 11
Solution:-
From the question, it is given that x = 2
We have,
= 8x – 4 + 3x + 11
= 11x + 7
Then, substitute the value of x in the equation.
= (11 × 2) + 7
= 22 + 7
= 29
7. Simplify these expressions and find their values if x = 3, a = – 1, b = – 2.
(i) 3x – 5 – x + 9
Solution:-
From the question, it is given that x = 3
We have,
= 3x – x – 5 + 9
= 2x + 4
Then, substitute the value of x in the equation.
= (2 × 3) + 4
= 6 + 4
= 10
(ii) 2 – 8x + 4x + 4
Solution:-
From the question, it is given that x = 3
We have,
= 2 + 4 – 8x + 4x
= 6 – 4x
Then, substitute the value of x in the equation.
= 6 – (4 × 3)
= 6 – 12
= – 6
(iii) 3a + 5 – 8a + 1
Solution:-
From the question, it is given that a = -1
We have,
= 3a – 8a + 5 + 1
= – 5a + 6
Then, substitute the value of a in the equation.
= – (5 × (-1)) + 6
= – (-5) + 6
= 5 + 6
= 11
(iv) 10 – 3b – 4 – 5b
Solution:-
From the question, it is given that b = -2
We have,
= 10 – 4 – 3b – 5b
= 6 – 8b
Then, substitute the value of b in the equation.
= 6 – (8 × (-2))
= 6 – (-16)
= 6 + 16
= 22
(v) 2a – 2b – 4 – 5 + a
Solution:-
From the question, it is given that a = -1, b = -2
We have,
= 2a + a – 2b – 4 – 5
= 3a – 2b – 9
Then, substitute the value of a and b in the equation.
= (3 × (-1)) – (2 × (-2)) – 9
= -3 – (-4) – 9
= – 3 + 4 – 9
= -12 + 4
= -8
8. (i) If z = 10, find the value of z3 – 3(z – 10).
Solution:-
From the question, it is given that z = 10
We have,
= z3 – 3z + 30
Then, substitute the value of z in the equation.
= (10)3 – (3 × 10) + 30
= 1000 – 30 + 30
= 1000
(ii) If p = – 10, find the value of p2 – 2p – 100
Solution:-
From the question, it is given that p = -10
We have,
= p2 – 2p – 100
Then, substitute the value of p in the equation.
= (-10)2 – (2 × (-10)) – 100
= 100 + 20 – 100
= 20
9. What should be the value of a if the value of 2x2 + x – a equals to 5, when x = 0?
Solution:-
From the question, it is given that x = 0
We have,
2x2 + x – a = 5
a = 2x2 + x – 5
Then, substitute the value of x in the equation.
a = (2 × 02 ) + 0 – 5
a = 0 + 0 – 5
a = -5
10. Simplify the expression and find its value when a = 5 and b = – 3.
2(a2 + ab) + 3 – ab
Solution:-
From the question, it is given that a = 5 and b = -3
We have,
= 2a2 + 2ab + 3 – ab
= 2a2 + ab + 3
Then, substitute the value of a and b in the equation.
= (2 × 52 ) + (5 × (-3)) + 3
= (2 × 25) + (-15) + 3
= 50 – 15 + 3
= 53 – 15
= 38
Exercise 12.4 Page: 246
1. Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.
If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern. How many segments are required to form 5, 10, 100 digits of the kind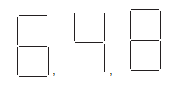 
Solution:-
(a)
From the question, it is given that the number of segments required to form n digits of the kind
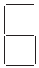is (5n + 1)
Then,
The number of segments required to form 5 digits = ((5 × 5) + 1)
= (25 + 1)
= 26
The number of segments required to form 10 digits = ((5 × 10) + 1)
= (50 + 1)
= 51
The number of segments required to form 100 digits = ((5 × 100) + 1)
= (500 + 1)
= 501
(b)
From the question, it is given that the number of segments required to form n digits of the kind
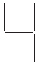is (3n + 1)
Then,
The number of segments required to form 5 digits = ((3 × 5) + 1)
= (15 + 1)
= 16
The number of segments required to form 10 digits = ((3 × 10) + 1)
= (30 + 1)
= 31
The number of segments required to form 100 digits = ((3 × 100) + 1)
= (300 + 1)
= 301
(c)
From the question, it is given that the number of segments required to form n digits of the kind
is (5n + 2)
Then,
The number of segments required to form 5 digits = ((5 × 5) + 2)
= (25 + 2)
= 27
The number of segments required to form 10 digits = ((5 × 10) + 2)
= (50 + 2)
= 52
The number of segments required to form 100 digits = ((5 × 100) + 1)
= (500 + 2)
= 502
2. Use the given algebraic expression to complete the table of number patterns.
| S. No. | Expression | Terms | |||||||||
| 1st | 2nd | 3rd | 4th | 5th | … | 10th | … | 100th | … | ||
| (i) | 2n – 1 | 1 | 3 | 5 | 7 | 9 | – | 19 | – | – | – |
| (ii) | 3n + 2 | 5 | 8 | 11 | 14 | – | – | – | – | – | – |
| (iii) | 4n + 1 | 5 | 9 | 13 | 17 | – | – | – | – | – | – |
| (iv) | 7n + 20 | 27 | 34 | 41 | 48 | – | – | – | – | – | – |
| (v) | n2 + 1 | 2 | 5 | 10 | 17 | – | – | – | – | 10001 | – |
Solution:-
(i) From the table (2n – 1)
Then, 100th term =?
Where n = 100
= (2 × 100) – 1
= 200 – 1
= 199
(ii) From the table (3n + 2)
5th term =?
Where n = 5
= (3 × 5) + 2
= 15 + 2
= 17
Then, 10th term =?
Where n = 10
= (3 × 10) + 2
= 30 + 2
= 32
Then, 100th term =?
Where n = 100
= (3 × 100) + 2
= 300 + 2
= 302
(iii) From the table (4n + 1)
5th term =?
Where n = 5
= (4 × 5) + 1
= 20 + 1
= 21
Then, 10th term =?
Where n = 10
= (4 × 10) + 1
= 40 + 1
= 41
Then, 100th term =?
Where n = 100
= (4 × 100) + 1
= 400 + 1
= 401
(iv) From the table (7n + 20)
5th term =?
Where n = 5
= (7 × 5) + 20
= 35 + 20
= 55
Then, 10th term =?
Where n = 10
= (7 × 10) + 20
= 70 + 20
= 90
Then, 100th term =?
Where n = 100
= (7 × 100) + 20
= 700 + 20
= 720
(v) From the table (n2 + 1)
5th term =?
Where n = 5
= (52 ) + 1
= 25+ 1
= 26
Then, 10th term =?
Where n = 10
= (102 ) + 1
= 100 + 1
= 101
So, the table is completed below.
| S. No. | Expression | Terms | |||||||||
| 1st | 2nd | 3rd | 4th | 5th | … | 10th | … | 100th | … | ||
| (i) | 2n – 1 | 1 | 3 | 5 | 7 | 9 | – | 19 | – | 199 | – |
| (ii) | 3n + 2 | 5 | 8 | 11 | 14 | 17 | – | 32 | – | 302 | – |
| (iii) | 4n + 1 | 5 | 9 | 13 | 17 | 21 | – | 41 | – | 401 | – |
| (iv) | 7n + 20 | 27 | 34 | 41 | 48 | 55 | – | 90 | – | 720 | – |
| (v) | n2 + 1 | 2 | 5 | 10 | 17 | 26 | – | 101 | – | 10001 | – |